Value at Risk (VaR) ist eine einzige, aussagekräftige Kennzahl im Risikomanagement, die den möglichen durchschnittlichen Verlust eines Finanzportfolios über einen definierten Zeitraum quantifiziert.
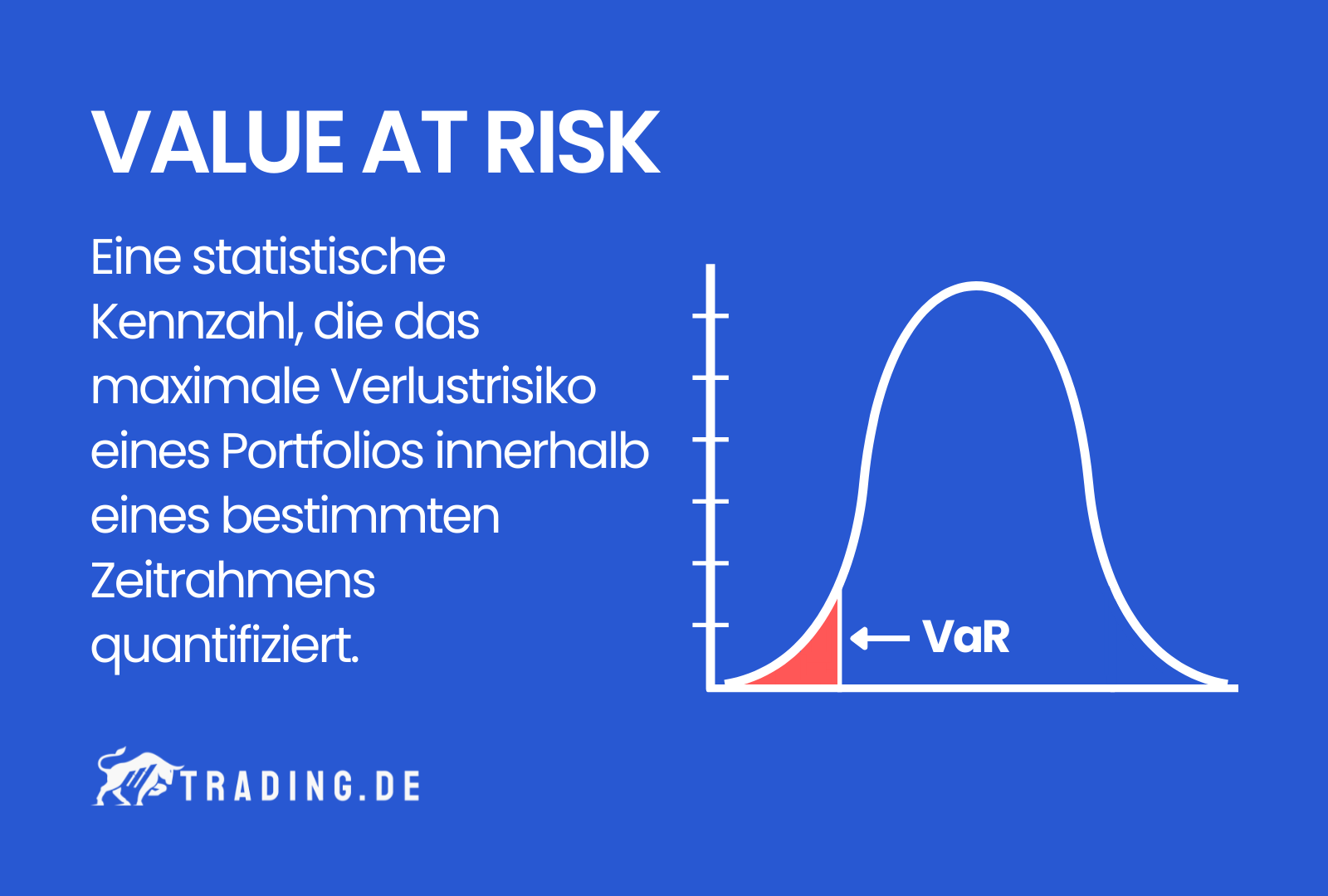
Value at Risk (VaR) kurz und knapp
- Der VaR ermöglicht die Bewertung von Aktienschwankungen und hilft, Portfolios strategisch zu optimieren.
- Die Entstehung von VaR reicht bis ins Jahr 1922 zurück, wurde jedoch erst in den 1980er Jahren relevant.
- Die Berechnung des VaR erfolgt durch die Quantifizierung potenzieller Verluste bei einem bestimmten Konfidenzniveau.
- VaR hat Vorzüge wie die Messung verschiedener Finanzinstrumente, aber auch Nachteile wie Abhängigkeiten und vereinfachte Annahmen.
Wie ist die Anwendung des Value at Risk (VaR)?
Im Gegensatz zu vielen statistischen Risiko-Kennzahlen bietet der VaR eine klare und effiziente Methode zur Bewertung von Aktienschwankungen. Es handelt sich um eine risikobasierte Messgröße, die keine Aussage über den maximalen Verlust trifft, sondern vielmehr dazu dient, das Portfolio strategisch günstiger zu gestalten.
Der VaR ermöglicht die Überwachung und Messung von Marktrisiken sowie Zinsrisiken und wird trotz statistischer Limitationen aufgrund seiner einfachen Anwendbarkeit und Verständlichkeit häufig genutzt. Ursprünglich aus dem Bedürfnis nach einem einheitlichen Risikobericht entstanden, definiert der VaR den absoluten Wertverlust einer Risikoposition mit einer vordefinierten Wahrscheinlichkeit innerhalb eines festen Zeitraums.
Was ist die Geschichte von Value at Risk (VaR)?
Die Entstehungsgeschichte von Value at Risk (VaR) lässt sich bis ins Jahr 1922 zurückverfolgen, als die New York Stock Exchange Kapitalanforderungen für Mitgliedsfirmen einführte. Erst in den späten 1980er Jahren wurde VaR relevant. Der Börsenkrach von 1987 löste eine systematische Abgrenzung von extremen Ereignissen aus, und die Bankers Trust entwickelte vor 1990 eine rudimentäre VaR-Messung, jedoch ohne standardisierten Namen oder Definition.
Die mathematischen Grundlagen des VaR wurden durch Harry Markowitz und andere im Kontext der Portfoliotheorie gelegt.
J.P. Morgan ermöglichte 1995 öffentlichen Zugang zu Varianzen und Kovarianzen verschiedener Sicherheiten und Anlageklassen, was zur Entwicklung von Risikomesssoftware führte. Der Begriff “Value at Risk” wurde von J.P. Morgan geprägt und populär gemacht, fand Anklang bei Banken und Regulierungsbehörden.
Wie ist die Berechnung des Value at Risk (VaR)?

Die Value-at-Risk (VaR)-Formel für eine Aktie kann auf verschiedene Weisen berechnet werden, wobei die grundlegende Idee darin besteht, die potenziellen Verluste in einem bestimmten Zeitraum bei einem gegebenen Konfidenzniveau zu quantifizieren. Typische Konfidenzniveaus sind 95 % und 99 %. Für den VaR einer Aktie wird oft der Zeitraum eines Jahres interessant. Bei einem Konfidenzniveau von 95 % ergibt sich ein Z-Wert von 1,6449 und bei einem Konfidenzniveau von 99 % ein z-Wert von 2,3263.
Eine einfache Möglichkeit ist die Verwendung der folgenden Formel:
Beispiel
- Kurs von Aktie XY: 100 €
- Volatilität: 20 %
- z-Wert: 95 %
Daraus ergibt sich, dass der Kursverlust der Aktie XY innerhalb eines Jahres wahrscheinlich nicht größer als 32,90 € sein wird. Diesen Wert kann man für jede Aktie im Portfolio berechnen und alle miteinander in Beziehung setzen.
Value at Risk (VaR): Vor- und Nachteile
Die Bewertung von Risiken durch den Value at Risk (VaR) bringt sowohl Vorteile als auch Nachteile mit sich. Die folgende Tabelle stellt diese in übersichtlicher Form dar:
Vorteile des VaR
- Kann das Risiko verschiedener Finanzinstrumente wie Aktien, Anleihen, Rohstoffe, Devisen und Derivate messen, um Anlegern zu helfen, Verluste zu vermeiden.
- Ermöglicht Vergleich von Risiken über verschiedene Anlageklassen und Portfolios
- Zukunftsorientiert und berücksichtigt Dichte der Wahrscheinlichkeitsverteilung in Gauß’scher Form
Nachteile des VaR
- Abhängig von mehreren Faktoren für eine genaue Berechnung
- Erfordert Zerlegung der Risiken in Einzelkategorien
- Kenntnis oder Schätzung von Abhängigkeiten erforderlich
- Notwendigkeit einer ausreichenden Datenlage
- Datenlage muss sich auf Einzelrisiken und deren Entwicklung beziehen
- Gibt keine Informationen über maximalen Verlust, sondern nur die Wahrscheinlichkeit eines Verlustes innerhalb eines Zeitraums
- Vereinfacht Realität durch Annahme einer Gauß’schen Verteilung, was extreme Verluste nicht abbilden kann
Fazit
Kursschwankungen sind normal, dennoch sind die Schwankungen vergangener Jahrzehnte größeren Extremen ausgesetzt. Methoden, um das Risiko zu minimieren, sind also verständlich. Obwohl statistische Berechnungen nur eine Wahrscheinlichkeit ausdrücken können, und je nach Wahl der statistischen Methode, jedes Modell an Grenzen stößt, da es nur gewisse Szenarien abbilden kann, kann die Statistik dabei helfen, einen objektiveren Blick auf das Risiko zu werfen. Eine Möglichkeit der Risikobewertung ist der VaR.
Der Vorteil des VaR ist seine leichte Verständlichkeit. Man bekommt sehr schnell ein Gefühl für ein Risiko. Es wird dabei ein statistisch wahrscheinliches Risiko eines Verlustes innerhalb eines Zeitraumes, meist ein Jahr, berechnet. Schnell ist so ein Vergleich möglich, und ein Portfolio kann schnell eingeschätzt werden.
Allerdings eignet sich der VaR nicht für Industrie- und Handelsunternehmen. In Finanzbereichen ist er aber gut anwendbar. Wobei berücksichtigt werden muss, dass der VaR keine Extremsituationen berücksichtigen kann.



